European Option Pricing Models

 This page contains the preview of the European option pricing models available in VBA Package Set 3.  The complete programs are available in open source codes.

This document contains information on the following option pricing models:

European Option Model on Asset with Known Cash Payouts

When a stock issues dividend, cash is paid to the holder of the asset.  The call holder does not receive any part of the payout.  When the stock goes ex-dividend, its value will usually decreased by approximately the amount of the dividend distribution.  Consider a stock that is expected to pay out  one dividend of Q amount on N date before the option expiration date.  On N date, the stock price will drop by Q amount in price. 

To take this dividend effect into account, we can substract the stock price by the present value of the dividend paid.  This is as if the stock did not pay out any dividend, but only began with a lower price.  The new S price, S*, would be original stock price minus the present value of all future dividends. 

The following demostrates the computation of option prices with the underlying asset that pays dividends.  Suppose the underlying asset pay dividend 3 times before the option expired.  The present value of these payouts is $8.95.  We discount the stock price by this amount and get $91.05.  This is the new stock price that we use to compute the option prices.  The option price model used for this example is the same as the model used in the Black-Scholes European Option Pricing Model example.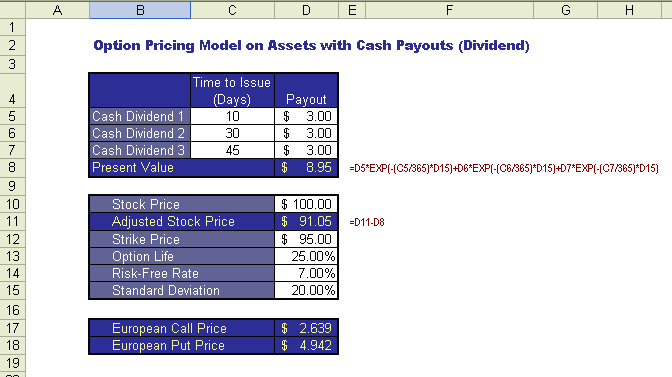



The delta for call and put are computed as0.4208 and -0.5792, respectively.

 


European Option Model on Asset with Continuous Cash Payouts (Index Option)

Some assets have numerous distribution of cash payouts.  An example is a broad-based stock market index portfolio (say SP500), in which nearly everyday one component stock or another will pay a dividend.   Merton (1973) has derived a variant of the Black-Scholes model for an asset that pays dividends continuously.  The payput can be treated as a constant proportion of the asset price.

The following demonstrates the computation of option prices with the underlying asset that pays continuous dividends.  Suppose dividend yield before the option expired is 10%.  Based on all other parameters value, the call price and the put price are, $6.254 and $2.075, respectively.  The delta for the call and put are 0.6702 and -0.3074, respectively.



European Option Model on Currency

In 1983, Garman and Kohlhagen developed a model that computes European currency options.   The following demostrates the computation of Currency option prices.  Based on the parameters value, the call price and the put price are, $0.333 and $0.097, respectively.  The delta for the call and put are 0.6818 and -0.2599, respectively.



European Option Model on Futures

Black in 1976, developed a variant of his basic model that can be applied to compute options on futures and forward contracts.

The following demostrates the computation of futures option prices.  Based on the parameters value, the call price and the put price are, $3.371 and $1.516, respectively.  The delta for the call and put are 0.6212 and -0.3066, respectively.